Wstęp

Czy zastanawialiście się kiedyś, skąd wyszukiwarki „wiedzą”, co użytkownik miał na myśli pomimo popełnionych literówek w wyszukiwanym haśle? Odpowiedzią są algorytmy obliczające miarę odmienności napisów. W tym artykule, postaram się omówić jeden z nich, jak również spróbować zoptymalizować go tak, aby był bardziej użyteczny dla rozwiązań informatycznych.

Odległość Levenshteina

Odległość Levenshteina – bo o tym algorytmie dzisiejszy wpis będzie – jest to prosty algorytm wyznaczający miarę odmienności napisów, czyli w uproszczeniu wyznacza ilość operacji prostych, które muszą zostać wykonane, aby słowo A stało się słowem B. Operacja prosta, w tym przypadku to:

• wstawienie nowego znaku
• usunięcie znaku
• podmienienie znaku

Dla zobrazowania, aby napis „kot” stał się napisem „mol” potrzebujemy wykonać 2 operacje proste – zamienić literkę „k” na „m” oraz „t” na „l”. Więc miara odmienności słowa „kot” i „mol” jest równa 2.

Algorytm

Jak więc nauczyć komputer, aby też potrafił rozpoznawać tę różnicę w słowach? Władimir Lewensztejn zaproponował poniższy algorytm:

1. Określamy długość badanych słów, długość słowa głównego A to `m`, a długość słowa porównywalnego B to `n`.

2. Tworzymy macierz(tablicę) `K` o wymiarach (m+1) x (n+1) .

3. Pierwszy wiersz macierzy wypełniamy wartościami od 0 do `n`

4. Pierwszą kolumnę macierzy wypełniamy wartościami od 0 do `m`

5. Dla każdego znaku słowa A wykonaj (od 1 do `m`, ozn. Indeksu `i`):

6. Dla każdego znaku słowa B wykonaj (od 1 do `n`, ozn. Indeksu `j`):

◦ jeżeli `A[i]` jest taki sam tak `A[j]` to koszt jest równy zero, w przeciwnym wypadku koszt jest równy 1
◦ przypisujemy wartość pola macierzy `K[i][j]` obliczając minimalną wartość z:
▪ `K[i – 1][j – 1]` + koszt
▪ `K[i – 1][j]` + 1
▪ `K[i][j – 1]` + 1

7. Miarą odmienności jest wartość wpisana w `K[m][n]`

Stosując powyższy algorytm, przeanalizujmy słowa „kot” i „pole”:

1. Długość słów m → 3, n → 4

2. 3. 4. Tworzymy macierz z wypełnionymi wartościami.

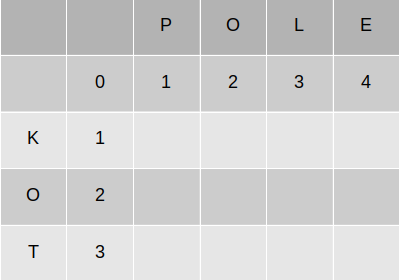
5. Obliczamy wartości macierzy.

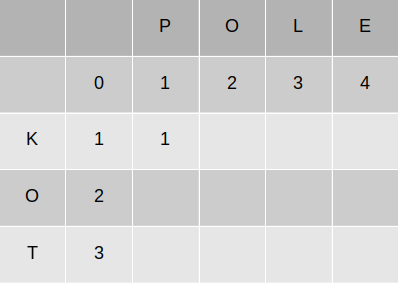
Znak P różni się od K więc koszt jest równy 1. Obliczamy wartości:

• `K[2 – 1][2]` + 1 = 2

• `K[2][2 – 1]` + 1 = 2

• `K[2 – 1][2 – 1]` + 1(koszt) = 1

Najmniejsza wartość to 1, więc tyle wpisujemy w pole `K[2][2]`.

Podobnie uzupełniamy resztę wartości z wiersza.

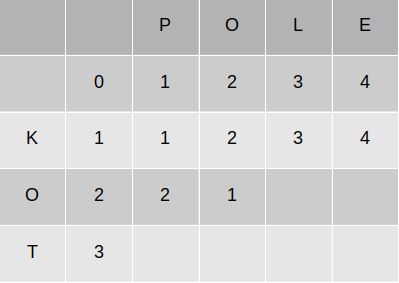
W tym przypadku znaki się od siebie nie różnią, więc koszt jest równy 0. Więc:

• `K[3 – 1][3]` + 1 = 3

• `K[3][3 – 1]` + 1 = 3

• `K[3 – 1][3 – 1]` + 0 = 1

I wpisujemy w pole `K[3][3]` wartość 1.

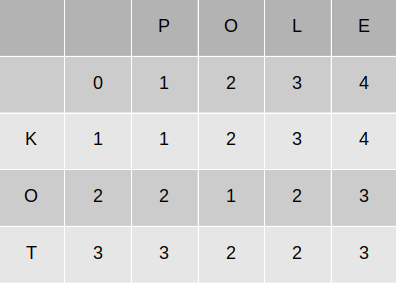
Implementacja

Implementacja algorytmu jest wkompilowana w interpreter PHP od wersji 4.0.1. Na potrzeby testów i optymalizacji zaimplementowałem go i można znaleźć go w repozytorium: https://gitlab.com/dysan12/levenshtein_distance

Optymalizacja

Wykonując krokowo algorytm, możemy zauważyć pewną zależność, dzięki której nie musimy wykonać wszystkich obliczeń, aby szacować odmienności podanych napisów. Wystarczy, że przy graficznej interpretacji „poprowadzimy” ukośną linię z wynikowego narożnika macierzy.

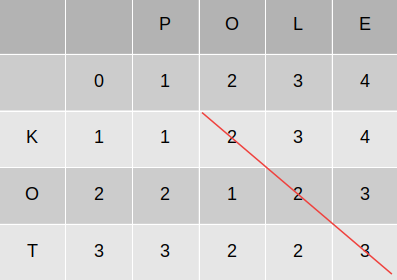
W tym wypadku, już po uzupełnieniu pierwszego wiersza, wiemy że odmienność napisów, będzie wynosiła co najmniej 2.

Szacunek ten możemy przykładowo wykorzystać w sytuacji, gdy chcemy poznać wszystkie słowa z pewnego zbioru, których odmienność od badanego słowa nie będzie większa od zadanej.

Implementacja

Przyjmując kontynuację algorytmu krokowego oraz , że `max` to zadana maksymalna różnica słów:
Dodajemy do każdej iteracji kroku piątego warunki kończące wykonywanie

• jeśli porównywane słowa mają taką samą długość, to sprawdź czy wartość `K[i][j]` > `max`
• jeśli słowo porównywane B jest dłuższe niż słowo główne A, to sprawdź czy wartość `K[i][i + n – m]` > `max`
• jeśli słowo porównywane B jest krótsze niż słowo główne A, to sprawdź czy wartość `K[i][i – (n – m)]` > `max`

Jeśli algorytm przedwcześnie zakończył swoją pracę, tzn. że badane słowa zbyt różnią się od siebie.

Ilustracja 1: Optymalizacja zrealizowana w PHP

Wyniki

Testy zostały przeprowadzone na ponad 1000 elementowym zbiorze porównywanych słów z wyznaczoną maksymalną odległością od 0 do 10.

Aspekty:

• zoptymalizowany algorytm vs algorytm bez optymalizacji
• zoptymalizowany algorytm vs wbudowany w PHP(bez optymalizacji)

Gdzie:

• „Optimized algorithm time” to czas wykonania zoptymalizowanego algorytmu
• „Standard algorithm time” to czas wykonania algorytmu bez optymalizacji
• „Saved time” to zaoszczędzony czas
• „Percentage ratio” to stosunek czasów. Jeśli wartość jest mniejsza niż 100% to zoptymalizowany algorytm wykonywał się dłużej.

Zoptymalizowany algorytm vs algorytm bez optymalizacji

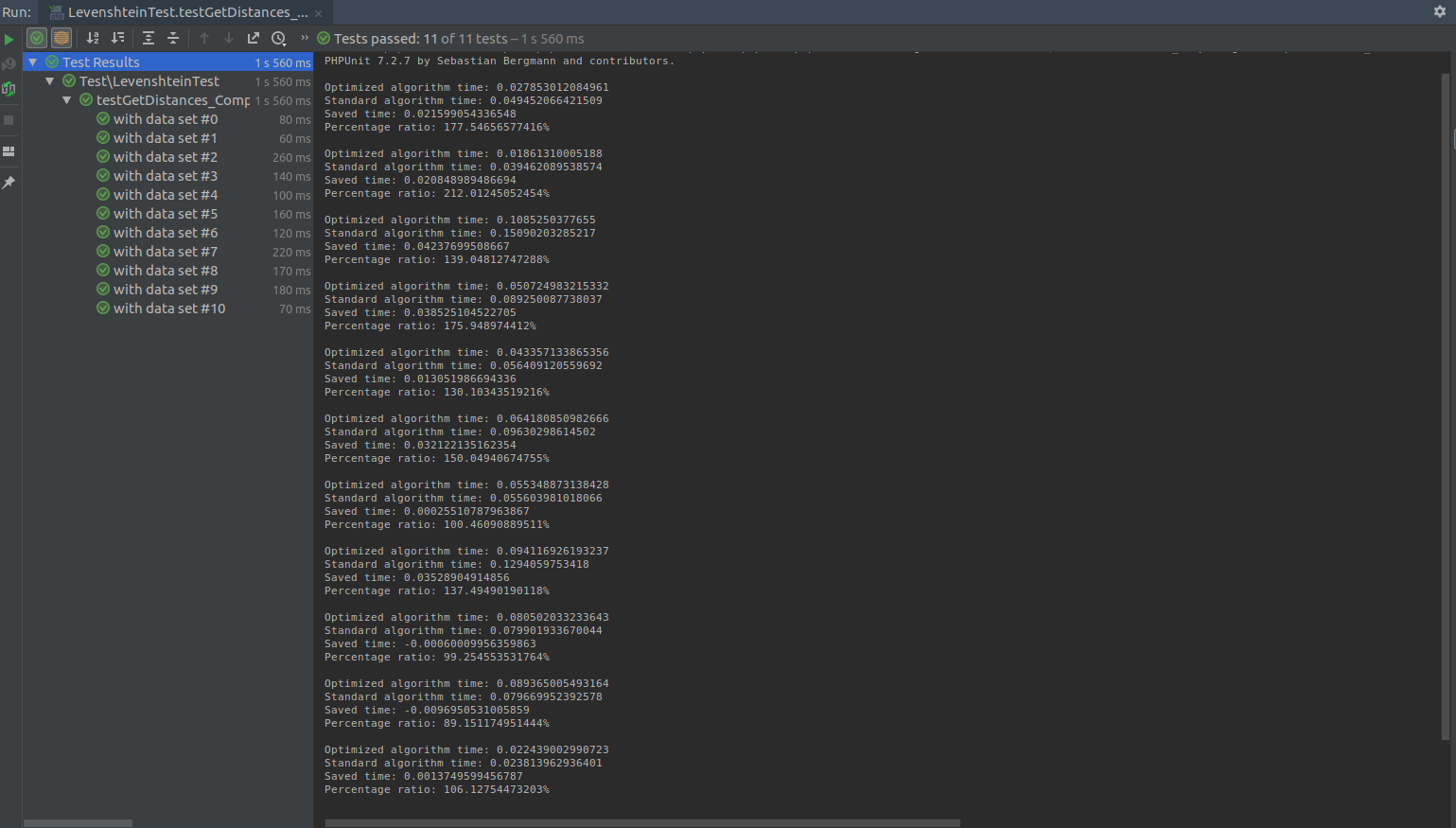
Z wyników widzimy, że optymalizacja, przy niskiej zadanej maksymalnej odległości, polepsza do 212% wydajność co daje ponad dwukrotnie skrócony czas obliczania.

Zoptymalizowany algorytm vs wbudowany w PHP(bez optymalizacji)

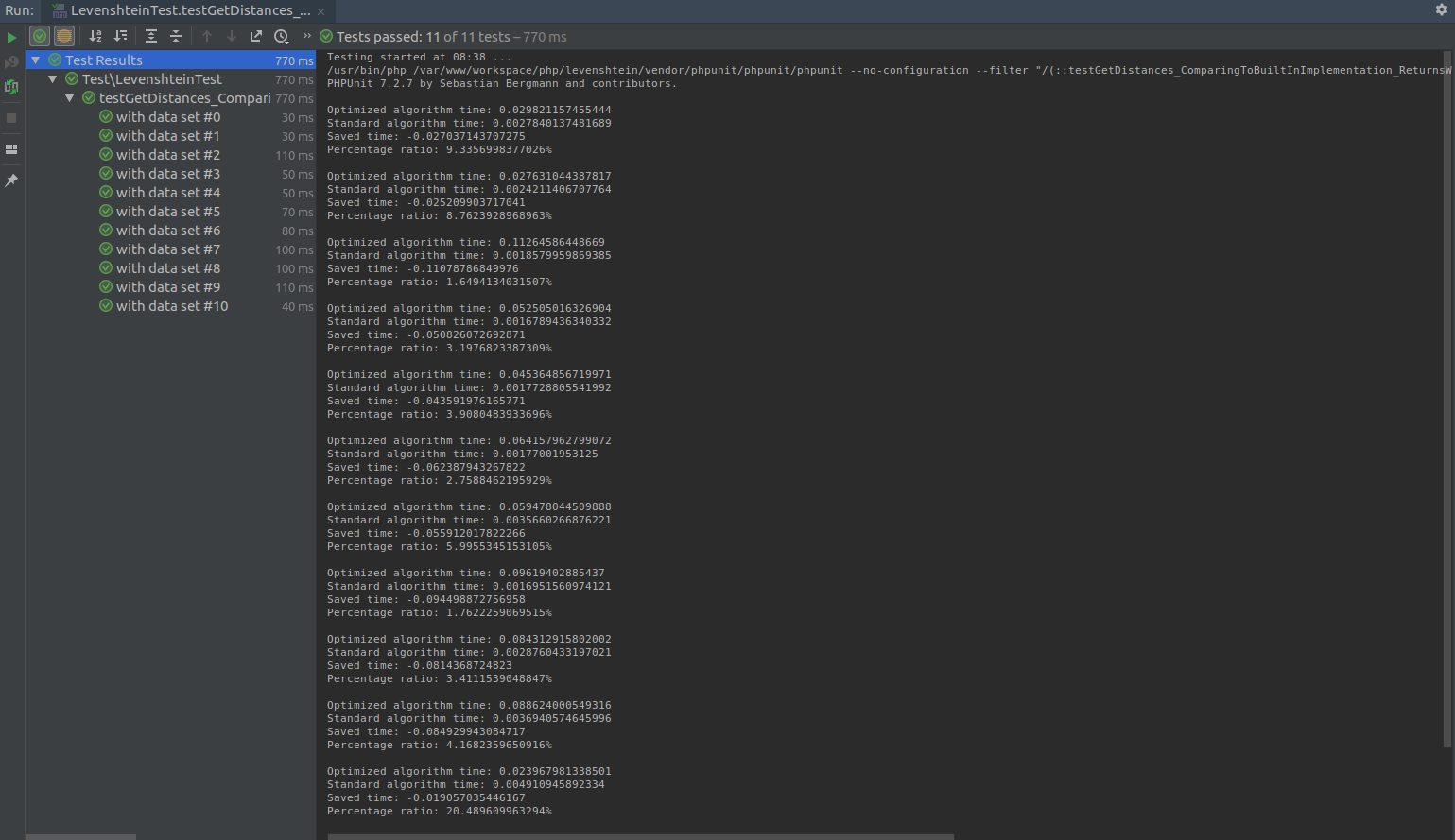
Wbudowana funkcja obliczania odległości levenshteina jest skompilowana w interpreter PHP, przez co wydajnościowo jest niejednokrotnie ponad 80 razy szybsza niż nieskompilowany algorytm – co nie było zaskoczeniem.

Wszystkie testy wraz z badanym zbiorem danych znajdują się w
https://gitlab.com/dysan12/levenshtein_distance/blob/master/test/LevenshteinTest.php

Podsumowanie optymalizacji

Z przeprowadzonych testów widzimy, że optymalizacja rzeczywiście skraca czas wykonania algorytmu, lecz aby z niej w praktyce skorzystać w języku interpretowanym, musielibyśmy wkompilować ją w interpreter.

Autorem tekstu jest Michał Gaj.